Le cours⚓
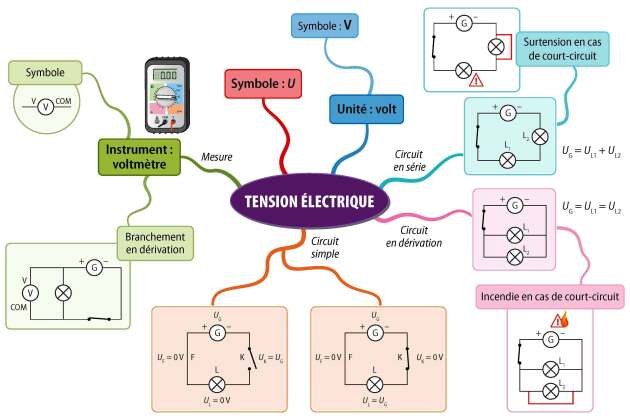
Partie 1 - La tension électrique⚓
Rappel : La tension électrique
ETC130 - Grandeurs électriques (partie sur la tension électrique et notamment les vidéos pour comprendre ce qu'est la tension et l'intensité)
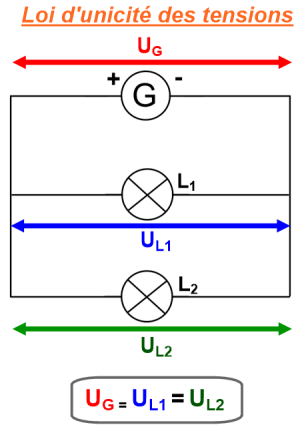
Définition : Dans les circuits en dérivation : Loi d'unicité
En dérivation la tension des dipôles obéit à la loi d’unicité des tensions : la tension aux bornes de dipôles branchés en dérivation est la même. Autrement la tension est unique (et égale à celle du générateur) pour des dipôles branchés sur les même noeuds.
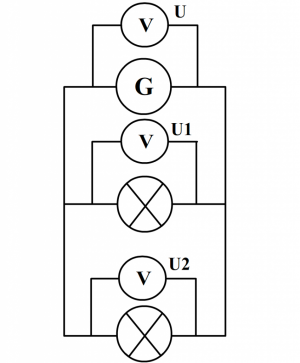
Exemple :
On mesure la tension entre les bornes de la lampes \(L_1\) dans le circuit en dérivation photographié ci-dessous. Quelle sera la tension entre les bornes de la lampe \(L_2\) ? Et entre les bornes du générateur ?
Il s'agit d'un circuit en dérivation (les points A et B sont les noeuds du circuit).
La loi d'unicité des tensions s'applique. La tension aux bornes des dipôles branchés sur les mêmes noeuds ont une même tension.
La tension entre les bornes de la lampe \(L_2\) sera donc égale à celle du générateur et on peut écrire que \(U_G = U_{L1} = U_{L2} = 4,51 V\).
Définition : Dans les circuits en série : Loi d'additivité
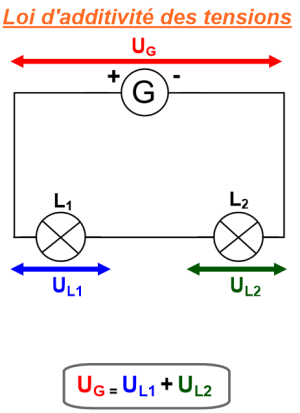
Dans un circuit en série, où les récepteurs sont reliés à un générateur, la somme des tensions de tous les récepteurs est égale à la tension du générateur. On parle de la loi d'additivité des tensions dans un circuit en série.
Exemple :
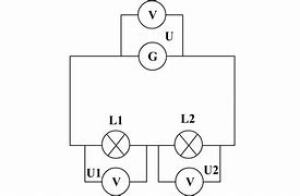
On mesure la tension entre les bornes du générateur (\(U_G = 7,59 V\)) et la tension entre les bornes de la lampe \(L_1\) (\(U_{L_1} = 7,14 V\)) dans le circuit en série photographié ci-dessous. Quelle sera la tension entre les bornes de la lampe \(L_2\) ?
Il s'agit d'un circuit en série donc la loi d'additivité des tensions s'applique. La somme des tensions des récepteurs branchés en série est égale à la tension aux bornes du générateur. On peut donc écrire que \(U_G = U_{L_1} + U_{L_2}\). Avec les valeurs mesurées cela devient \(7,59 V = 7,14 V + U_{L_2}\). On peut donc en déduire la valeur de la tension aux bornes de la lampe \(L_2\). \(U_{L_2} = U_G - U_{L_1} = 7,59 V - 7,14 V = 0,45 V\).
La tension aux bornes de la lampe \(L_2\) est donc de \(U_{L_2} = 0,45 V\).
Rappel : Petit bilan général sur la tension électrique
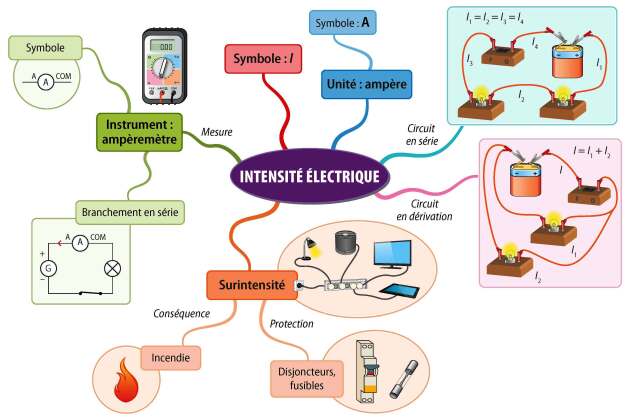
Partie 2 - L'intensité du courant électrique⚓
Rappel : L'intensité du courant
ETC130 - Grandeurs électriques (partie sur l'intensité du courant et notamment les vidéos pour comprendre ce qu'est la tension et l'intensité)
Définition : Dans les circuits en série : Loi d'unicité
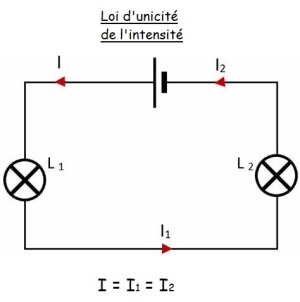
En série l'intensité obéit à la loi d’unicité de l'intensité : l'intensité qui traverse les dipôle à la même valeur en tout point du circuit.
Exemple :
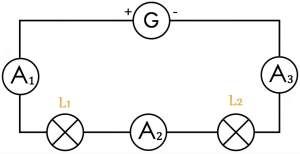
Dans un circuit en série, on mesure l'intensité du courant débitée par un pile. Quelles les valeurs mesurées par les deux autres ampèremètres ?
Il s'agit d'un circuit en série donc c'est la loi d'unicité de l'intensité qui s'applique. L'intensité sera de même valeur partout dans le circuit. On peut écrire que \(I = I_1 = I_2\) et les deux autres ampèremètres indiqueront une intensité de \(I = 0,05 A\).
Définition : Dans les circuits en dérivation : Loi d'additivité
En dérivation l'intensité obéit à la loi d’additivité des intensités : l'intensité dans la branche principale est égale à la somme des intensités des branches dérivées. Autrement dit, lorsque le courant électrique arrive à un noeud, il se sépare en deux parties qui s'ajoutent à l'autre noeud avant de retourner au générateur.
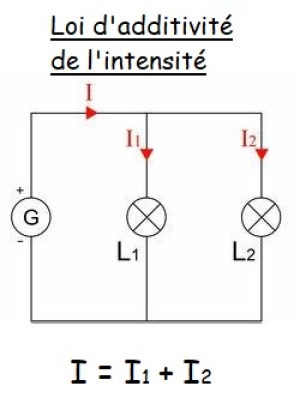
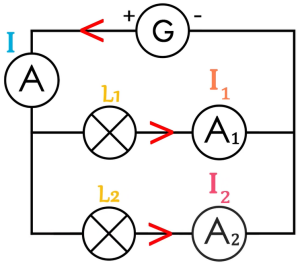
Exemple :
L'ampèremètre de gauche mesure l'intensité du courant débitée par la pile \(I = 0,29 A\). L'ampèremètre du milieu indique l'intensité traversant la lampe \(L_1\), \(I_{L_1} = 0,07 A\). Quelle sera la valeur de l'intensité mesurée par l'ampèremètre de droite, mesurant l'intensité du courant traversant la lampe \(L_2\) ?
Il s'agit d'un circuit en dérivation donc c'est la loi d'additivité des intensités qui s'applique. L'intensité de la branche principale est égale à la somme des intensités des branches dérivées. La lampe \(L_1\) est dans une branche dérivée et la lampe \(L_2\) dans un seconde branche dérivée. On peut écrire que \(I = I_{L_1 } + I_{L_2}\) soit \(0,29 A = 0,07 A + I_{L_2}\). On peut en déduire que \(I_{L_2} = 0,29 A - 0,07 A = 0,22 A\).
Rappel : Petit bilan général sur l'intensité du courant électrique
